Matemática I: Tipos de Funciones.

Identificación de Funciones Básicas.

Existen distintos tipos de funciones a los cuales se les identifican con las siguientes explicaciones y ecuaciones de las funciones básicas.

Función Lineal:

Decimos que existe una función lineal si y solo si en el plano cartesiano existen rectas horizontales o con pendientes, las rectas verticales no son funciones ya que estas mismas no justifican el criterio de la recta vertical.

 La pendiente se identifica con letra "m", ésta ayuda a conocer qué tanto esta la recta inclinada. mientras que la letra "b" inicialmente es el corte con el eje Y. Mas adelante veremos PRINCIPIOS DE GRAFICACIÓN, los cuales nos ayudaran a graficar una función.

Función Cuadrática:

Esta representada por una ecuación normalmente con tres termino, en donde la variable independiente (la variable  X) esta elevado a un grado igual a 2, siendo este el de grado mayor. Su gráfica representa una parábola, este puede estar cóncava hacia abajo o cóncava hacia arriba (Principios de Graficación).

Función Potencia Pura:

Esta es semejante a la anterior pero su estudio aplica a exponentes pares o impares. En las gráficas se pueden observar la diferencia de cada una de ellas. Su ecuación es sencilla ya que solo aparecerá la variable afectada por una suma o resta (ver Principios de Graficación).

En los dos casos la "n" es un número natural y mayor que 1.

Función Racional:

Este tipo de función, es en donde la variable se encuentra en el denominador, ellos también dependen de su exponente. Se expresan de manera básica como se muestran a continuación:

En los dos casos la "n" es un número natural y mayor que 1.

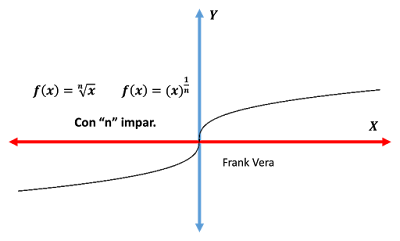
Función Radical:

En esta Función la Variable X esta bajo el dominio de un exponente enésimo, como se muestran junto a las figuras:

Es en donde la variable X se encuentra en una raíz,

Función Exponencial:

Deducimos o reconocemos fácilmente que una Función es Exponencial si la variable X, se encuentra como un exponente, para deducir sus cortes es necesario conocer las propiedades en donde ella se relaciona con la logarítmica. Sus gráficas son las siguientes:

Función Logarítmica:

La función logarítmica es la inversa de la exponencial, usando propiedades en las cuales intervienen la participación de ellas, se pueden graficar mas sencillamente sus funciones, su grafican dependen de los valores de la base:

Función Valor Absoluto

Se constituye a partir de cualquier función antes mencionada, solo que al aplicar un valor absoluto a las funciones, hará que ellas solo posean imágenes en el eje Y con valores positivos, esto se refiere que al terminar de realizar la graficación correspondiente a la función dada, debemos reflejar sobre la recta horizontal del Eje X, todo imagen que se encuentre debajo de ella. Mostraremos un ejemplo de como cambiaría el valor absoluto una función.